Answer:
We conclude that there is a significant difference in the proportion of all college students who would be embarrassed by these two admissions.
Explanation:
We are given that 462 of 500 randomly selected college students said they would be embarrassed to truthfully admit they could not read at a fourth grade level.
Further suppose 135 of 500 randomly selected college students said they would be embarrassed to truthfully admit they could not "do math" at a fourth grade level (like fractions).
Let
 = proportion of college students who would be embarrassed to truthfully admit they could not read at a fourth grade level.
= proportion of college students who would be embarrassed to truthfully admit they could not read at a fourth grade level.
 = proportion of college students who would be embarrassed to truthfully admit they could not "do math" at a fourth grade level.
= proportion of college students who would be embarrassed to truthfully admit they could not "do math" at a fourth grade level.
So, Null Hypothesis,
 :
:
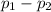 = 0 or
= 0 or
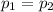 {means that there is not any significant difference in the proportion of all college students who would be embarrassed by these two admissions}
{means that there is not any significant difference in the proportion of all college students who would be embarrassed by these two admissions}
Alternate Hypothesis,
 :
:
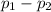
 0 or
0 or
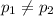 {means that there is a significant difference in the proportion of all college students who would be embarrassed by these two admissions}
{means that there is a significant difference in the proportion of all college students who would be embarrassed by these two admissions}
The test statistics that would be used here Two-sample z proportion statistics;
T.S. =
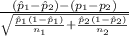 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of college students who would be embarrassed to admit they could not read at a fourth grade level =
= sample proportion of college students who would be embarrassed to admit they could not read at a fourth grade level =
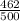 = 0.924
= 0.924
 = sample proportion of college students who would be embarrassed to admit they could not "do math" at a fourth grade level =
= sample proportion of college students who would be embarrassed to admit they could not "do math" at a fourth grade level =
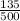 = 0.27
= 0.27
 = sample of college students = 500
= sample of college students = 500
 = sample of college students = 500
= sample of college students = 500
So, test statistics =
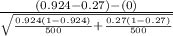
= 28.28
The value of z test statistics is 28.28.
Also, P-value of the test statistics is given by;
P-value = P(Z > 28.28) = Less than 0.0005%
Now, at 0.10 significance level the z table gives critical values of -1.645 and 1.645 for two-tailed test.
Since our test statistics doesn't lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.
Therefore, we conclude that there is a significant difference in the proportion of all college students who would be embarrassed by these two admissions.