Question

A architectural designer, Jenee, wishes to create a triangular garden for her client's business. The garden will be a right triangle with the smallest leg of a right triangle equal to 8 m. To be consistent with the design of the building, the other two sides of the triangular garden will form an arithmetic sequence. (Hint: Pythagorean equation)

What are the lengths of the two unknown sides?

Longest side /

Other side /



What is the perimeter of the garden?

Answer 1

The length of the longest side is 13.33

The length of the other side is 10.67

Explanation:

Here we have the lengths of the other two sides will form an arithmetic sequence as follows

`a_n = a_1 + (n-1)d`

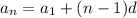
Therefore, the three sides will be of the form

a₁, a₁+d, a₁+2·d

However, we note that the smallest side is a₁ ∴ a₁ = 8

Hence, we have;

8, 8 + d, 8 + 2·d

Also the qustion notes that the triangle is a right angled triange, therefore, Pythagorean equation applies.

Pythagorean equation is

a² + b² = c²

Where:

c = The hypotenuse (the longest side) of the right triangle

Therefore

(8 + d)² + 8² = (8 + 2·d)²

Hence;

d²+16·d+128 = 4·d²+32·d·64

Which gives;

3·d²+16·d-64 =0

Factorizing, we get;

(3·d - 8)(d + 8) = 0

Therefore, d = -8 or d = 8/3

Since, d is a measured increase, therefore, d = 8/3

The other two sides are;

8 + 8/3 = 32/3 =
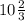`10\tfrac{2}{3}` and 8+2×8/3 = 40/3 =
`13\tfrac{1}{3}`

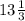
Hence the length of the longest side =
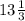`13\tfrac{1}{3}` = 13.33

The length of the other side =
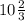`10\tfrac{2}{3}` = 10.67.