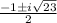Question

I need help with this and can I see the steps also?

Answer 1

Nico is incorrect because he added 3x instead of subtracting 3x from both sides.

`x=-(1+i√(23) )/(2) , -(1-i√(23) )/(2)`

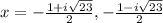
Explanation:

Ok, so first we need to get the equation set to 0 so we have a quadratic equation.

`4x+6=3x-x^(2) \\x^(2) +4x+6=3x\\x^(2)+x+6=0\\`

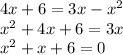
Here you would begin to factor but this is not possible with this equation. There is not a solution set that would be a product of 6 and a sum of 1. So you have to use the quadratic formula.

`\frac{-b\pm \sqrt{b^(2)-4ac } }{2a}`

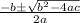
So if we look at our quadratic,

`(1)x^(2)+(1)x+6=0\\`

`ax^(2) +bx+c=0`

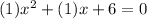
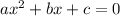
we know,

`a=1\\b=1\\c=6`

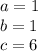
Now it's time to plug and play.

`\frac{-(1)\pm \sqrt{(1)^(2)-4(1)(6) } }{2(1)}\\(-1\pm √(1-24 ) )/(2)\\(-1\pm √(-23 ) )/(2)`

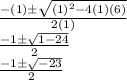
Ok, so it is impossible to have a negative root which means we have a complex number or imaginary number. We use
`i` to represent these imaginary numbers. We can't simplify the root anymore.

`(-1\pm i√(23 ) )/(2)`