Question

A health statistics agency in a certain country tracks the number of adults who have health insurance. Suppose according to the agency, the uninsured rates in a recent year are as follows: 5.4% of those under the age of 18, 12.8% of those ages 18–64, and 1.4% of those 65 and older do not have health insurance. Suppose 22.7% of people in the county are under age 18, and 61.9% are ages 18–64. (a) What is the probability that a randomly selected person in this country is 65 or older? (b) Given that a person in this country is uninsured, what is the probability that the person is 65 or older? (Round your answer to three decimal places.)

Answer 1

a) 15.4% probability that a randomly selected person in this country is 65 or older

b) 0.023 = 2.3% probability that the person is 65 or older

Explanation:

To solve b), i will use the Bayes Theorem.

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

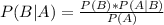
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

(a) What is the probability that a randomly selected person in this country is 65 or older?

22.7% of people in the county are under age 18

61.9% are ages 18–64

p% are 65 or older.

The sum of those is 100%. So

22.7 + 61.9 + p = 100

p = 100 - (22.7+61.9)

p = 15.4

15.4% probability that a randomly selected person in this country is 65 or older.

(b) Given that a person in this country is uninsured, what is the probability that the person is 65 or older?

Event A: Uninsured

Event B: 65 or older.

15.4% probability that a randomly selected person in this country is 65 or older.

This means that
`P(B) = 0.154`

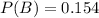
1.4% of those 65 and older do not have health insurance.

This means that
`P(A|B) = 0.014`

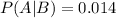
Probability of not having insurance.

22.7% are under 18. Of those, 5.4% do not have insurance.

61.9% are aged 18-64. Of those, 12.8% do not have insurance.

15.4% are 65 or over. Of those, 1.4% do not have health insurance. So

`P(A) = 0.227*0.054 + 0.619*0.128 + 0.154*0.014 = 0.093646`

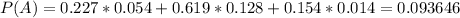
Then

`P(B|A) = (0.154*0.014)/(0.093646) = 0.023`

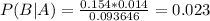
0.023 = 2.3% probability that the person is 65 or older