Question

In the diagram, DG = 15, GF = 5, EH = 12, and DE = 8. Triangle D F E is shown. Line segment G H is drawn from side D F to side E F to form triangle G F H. The length of D G is 15, the length of G F is 5, the length of E H is 12, and the length of D E is 8. To prove that △DFE ~ △GFH by the SSS similarity theorem using the information provided in the diagram, it would be enough additional information to know that HF is 2 units and GH is 3 units. HF is 3 units and GH is 2 units. HF is 4 units and GH is 2 units. HF is 3 units and GH is 4 units.

Answer 1

Answer: C

Explanation: Correct on Edgenuity. I got a 100%.

Answer 2

HF is 4 units and GH is 2 units. Option C is the right choice.

As per given information,

△ DFE
`\sim` △ GFH

Means △ DFE is same as of △ GFH.

So we can take the ration of the given sides of both the triangle.

`(DE)/(GH) = (DF)/(GF) = (EF)/(HF)`

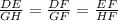
DF = DG +GF

DF = 15 + 5 = 20 UNITS

Put the given values in that ratio

`(8)/(GH)= (20)/(5)= (12+HF)/(HF)`

`(8)/(GH)= (4)/(1)= (12+HF)/(HF)`

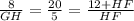
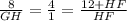
Separate it

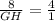`(8)/(GH)= (4)/(1)` and
`(4)/(1)= (12+HF)/(HF)`

`(8)/(GH)= (4)/(1)`

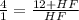
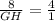
8 = 4 GH

After dividing both side by 4 we get

GH = 2 units

`(4)/(1)= (12+HF)/(HF)`

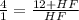
4 HF = 12 + HF

3 HF = 12

After dividing both side by 3 we get

HF = 4 units

So, Option C is the right choice.