Question

Question 1,2, and 3 how do i factor those? Can you show the work and explain how?

Answer 1

1:
`3n^(2)+9n+6`

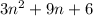
notice that each part is divisible by 3

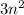`3n^(2)` ÷ 3 =
`n^(2)`

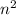
9n ÷ 3 = 3n

6 ÷ 3 = 2

so it becomes
`3(n^(2) +3n+2)`

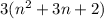
3n can be rewritten as 2n+n

-you want to rewrite it into two numbers that multiply to the number that's alone (in this case 2)

which would get you

`3(n^(2) +2n+n+2)`

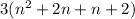
Now that it's rewritten, you can factor out n + 2 from the equation.

the answer is

3(n+2)(n+1)

And you can check that by multiplying (n+2)(n+1) which is
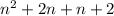`n^(2) +2n+n+2` and then each of those by 3, which is
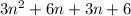`3n^(2) +6n+3n+6` or
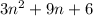`3n^(2)+9n+6`, our origional equation

2:
`28+x^(2) -11x`

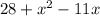
So I rewrote this as
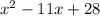`x^(2) -11x+28` (it's the same thing, just reordered using the commutative property)

now -11x can be rewritten as -4x-7x

(remember, the two numbers should multiply to equal 28, which is our constant.)

`x^(2) -4x-7x+28`

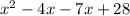
now we can factor out x from the first expression and -7 from the second

`x(x-4)-7(x-4)`

and lastly you factor out x-4,

which would give you

(x-4)(x-7)

Make sure to check your work and make sure it multiplies to
`x^(2) -11x+28`

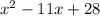
3:
`9x^(2) -12x+4`

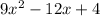
The first thing I notice when looking at this problem is that both 9 and 4 are perfect squares. Not only that, but they are the squares of 2 and 3, which are products of -12

So if you rewrite 9 as
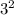`3^(2)` and 4 as
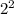`2^(2)`, the equation becomes

`3^(2) x^(2) -12x+2^(2)`

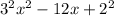
now that
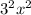`3^(2) x^(2)` is ugly so it can be turned into
`(3x)^(2)`

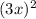
and -12x can be rewritten as
`-2*3x*2`

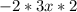
so our equation now looks like
`(3x)^2-2*3x*2+2^(2)`

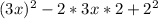
There's a rule that says
`a^(2) -2ab+b^(2) = (a-b)^(2)`

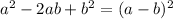
In our case, a=3x and b=2

so the final answer is

`(3x-2)^2`