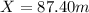Question

Circle towns limit form a perfectly circular shape that has a population of 20000 in the population density of 480 people per square kilometer what is circle X radius

Answer 1

`D =(P)/(\pi X^2)`

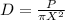
And solving for the radius we got:

`X = \sqrt{(P)/(\pi D)}`

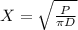
And replacing the data given we got:

`X = \sqrt{(480 (people)/(km^2))/(\pi *20000 people)}= 0.0874Km`

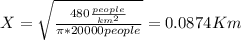
And this value converted to meters is
`X = 87.40 m`

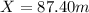
Explanation:

For this case we know the population size
`P = 20000` and we also know the population density
`D = 480 (people)/(km^2)`

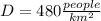
We can assume that the area is a circle. We also know that the formula for the population density is given by:

`D= (P)/(A)`

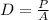
Where P represent the number of people and A the area. Since we are assuming a circle then the area is given by:

`A = \pi X^2`

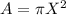
With X the radius of the circle

And then the populationd density become:

`D =(P)/(\pi X^2)`

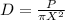
And solving for the radius we got:

`X = \sqrt{(P)/(\pi D)}`

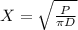
And replacing the data given we got:

`X = \sqrt{(480 (people)/(km^2))/(\pi *20000 people)}= 0.0874Km`

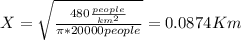
And this value converted to meters is
`X = 87.40 m`