Answer:
244 miles (nearest whole number)
Explanation:
This scenario can be modeled as a geometric series.
From the information given:
 (initial term) = 8 (miles)
(initial term) = 8 (miles)
 (common ratio) = 1.05 (as number of miles increases by 5% each week)
(common ratio) = 1.05 (as number of miles increases by 5% each week)
 = 19 (as the plan is for 19 weeks)
= 19 (as the plan is for 19 weeks)
The formula for the sum of the first n terms of a geometric series is:
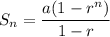
Therefore, the sum of the first 19 terms is:

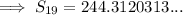
Solution
244 miles (to the nearest whole number)