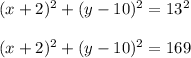Question

Circle C has a center at (-2,10) and contains the point P(10,5). Which equation represents circle C?

Answer 1

The equation that represents circle C is
`(x+2)^2+(y-10)^2=169`.

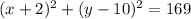Explanation:

A circle is the set of all points in the plane which maintains a fixed finite distance r from a fixed point O = (a, b). Here O is called the center, and r is called the radius of that circle.

The standard equation for a circle with center (a, b) and radius r is

`(x-a)^2+(y-b)^2=r^2`

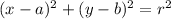
We are told that the center of this circle is (-2, 10), so

`(x+2)^2+(y-10)^2=r^2`

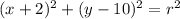
We are also told that the circle contains the point (10, 5), so we will use that information to find the radius r.

`(10+2)^2+(5-10)^2=r^2\\\\r^2=\left(10+2\right)^2+\left(5-10\right)^2\\\\r^2=12^2+5^2\\\\r^2=144+25\\\\r^2=169\\\\r=√(169)=13`

Therefore, the equation that represents circle C is

`(x+2)^2+(y-10)^2=13^2\\\\(x+2)^2+(y-10)^2=169`