Question

Determine which statement below is true about the volume of the two cylinders shown. * 15 points Captionless Image SCALE FACTOR = 3 so, the left has 6 times more volume than the right. SCALE FACTOR = 3 so, the left has 24 times more volume than the right. SCALE FACTOR = 3 so, the left has 9 times more volume than the right. SCALE FACTOR = 3 so, the left has 27 times more volume than the right.

Answer 1

(D)SCALE FACTOR = 3 so, the left has 27 times more volume than the right.

Explanation:

Given two similar cylinders, where the scale factor is 3.

Since the image is not here, I will illustrate using figures.

Smaller Cylinder

Radius =2cm, Height=3cm

Volume

`=\pi r^2h\\=\pi*2^2*3=12\pi cm^3`

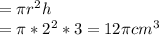
Larger Cylinder(Scale Factor of 3)

Radius =2X3=6cm, Height=3X3=9cm

Volume

`=\pi r^2h\\=\pi*6^2*9=324\pi cm^3`

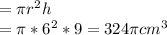
We can see that:

Volume of Larger Cylinder
`=27 X 12\pi =324\pi cm^3`

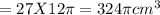
Therefore: Option D is the correct option.

In general, given similar solids, the ratio of their volume is:

1: Cube of the Scale Factor