Question

Dany jest punkt A(5,8) oraz punkt S(-1,-3) będący środkiem odcinka AB. Wyznacz współrzędne punktu B.

Answer 1

Hello can you translate the problem as I can’t understand what you are saying and I would be more than happy to help thank you

Answer 2

Since point S (-1, -3) is the midpoint of the segment AB, the coordinates of point B are (-7, -14).

In order to determine the midpoint of a line segment with two (2) end points, we would add each end point together and then divide by two (2):

`Midpoint=((x_1+x_2)/(2) ,(y_1+y_2)/(2) )`

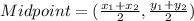
Next, we would determine the coordinate of B on line segment AB with midpoint S at (-1, -3). Let us substitute our given values into the midpoint formula as follows;

`(-1,-3)=((5+x_2)/(2) ,(8+y_2)/(2) )`

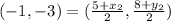
By setting up two equations to solve for our tow unknowns x₂ and y₂;

`-1=(5+x_2)/(2)\\\\-2=5+x_2\\\\x_2=-5-2\\\\x_2=-7`

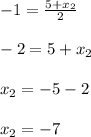
Therefore, the x-coordinate of end point B is -7.

For the y-coordinate of end point B on line segment AB, we have the following:

`-3=(8+y_2)/(2) \\\\-6=8+y_2\\\\y_2=-6-8\\\\y_2=-14`

In conclusion, the coordinates of point B are (-7, -14).

Complete Question:

The point A (5, 8) is given. Determine the coordinates of point B, knowing that the point S (-1,-3) is the midpoint of the segment AB.