Question

Annual sales for a fast food restaurant are $650,000 and are increasing at rate of 4% per year. Use an exponential function to find the annual sales after 7 years. The answer would be $855,355.66.

Answer 1

We have been given that annual sales for a fast food restaurant are $650,000 and are increasing at rate of 4% per year. We are asked to find the annual sales after 7 years using an exponential function.

We know that an exponential growth function is in form
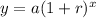`y=a(1+r)^x`, where,

y = Final amount,

a = Initial amount,

r = Growth rate in decimal form,

x = Time.

Let us convert 4% into decimal form.

`4\%=(4)/(100)=0.04`

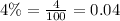
Initial value is $650,000.

`y=\$650,000(1+0.04)^x`

`y=\$650,000(1.04)^x`

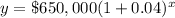
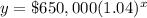
To find annual sales after 7 years, we will substitute
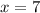`x=7` in our function as:

`y=\$650,000(1.04)^7`

`y=\$650,000(1.31593177923584)`

`y=\$855,355.656503296`

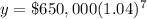
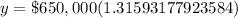
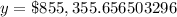
Upon rounding to nearest hundredths, we will get:

`y\approx \$855,355.66`

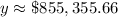
Therefore, the annual sales will be approximately
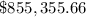`\$855,355.66` after 7 years.