Question

PLEASE HELP!!

it’s multiple choice but i never get any of the answers.

differentiate y=x^(e^x)

Answer 1

We are given the function to differentiate:

`{\quad \qquad \sf \rightarrow y=x^(e^x)}`

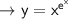
Do take natural log on both sides, then we will be having

`{:\implies \quad \sf ln(y)=ln(x^{e^(x)})}`

`{:\implies \quad \sf ln(y)=e^(x)ln(x)\quad \qquad \{\because ln(a^b)=bln(a)\}}`

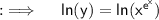
Now, differentiate both sides by using so called chain rule and the product rule

`{:\implies \quad \sf (1)/(y)(dy)/(dx)=e^(x)ln(x)+(e^x)/(x)}`

`{:\implies \quad \boxed{\bf{(dy)/(dx)=x^(e^x)\bigg\{(e^x)/(x)+ln(x)e^(x)\bigg\}}}}`

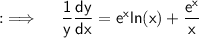
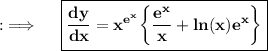
Hence, Option B) is correct

Product rule of differentiation:

• 
  `{\boxed{\bf{(d)/(dx)(uv)=u(dv)/(dx)+v(du)/(dx)}}}`

Where, u and v are functions of x