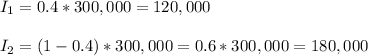Answer:
She have to invest at least $120,000 in the 12%-return asset and $180,000 in the 7%-asset to have an annual income of $27,000.
Explanation:
We will solve this as investing the minimum proportion in the risky investment (12% return), with the condition of having an annual income of $27,000.
The return can be calculated as:
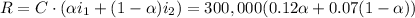
R: annual return, C: capital, α: proportion of the risky asset, i1: rate of return of the risky asset, i2: rate of return of the less risky asset.
Then, we can calculate the proportion of the risky asset as:

The proportion of the risky asset is 40%.
The investments in each asset will be: