Question

1. Consider a sphere with a radius of 18 inches.

Part A: Determine the surface area of the sphere.
Part B: Determine the volume of the sphere.
2. A sphere has a surface area of 2463 square centimeters. Find the diameter of the sphere

Answer 1

1. The surface area is
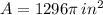`A=1296\pi \:in^2` and the volume is
`V=7776\pi \:in^3`.

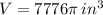2. The diameter of the sphere is
`d=\sqrt{(2463)/(\pi )}\approx 27.9999 \:cm`.

Explanation:

The surface area of a sphere is given by the formula

`A=4\pi r^2`

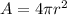
The volume enclosed by a sphere is given by the formula

`V=(4)/(3)\pi\cdot r^3`

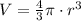
where
`r` is the radius of the sphere.

1. From the information given we know that the sphere has a radius of 18 inches.

The surface area is

`A=4\pi \left(18\right)^2\\\\A= 4\cdot \:324\pi\\\\A=1296\pi \:in^2`

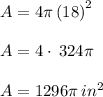
and the volume is

`V=(4)/(3)\pi \left(18\right)^3=(4\pi 18^3)/(3)=(3^6\cdot \:2^3\cdot \:4\pi )/(3)=7776\pi \:in^3`

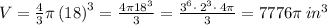
2. The diameter of a sphere is given by
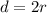`d=2r`, where
`r` is the radius of the sphere.

We know that the surface area is 2463 square centimeters. To find the diameter of the sphere first we need to find the the radius.

`A=4\pi r^2\\\\2463=4\pi r^2\\\\4\pi r^2=2463\\\\r^2=(2463)/(4\pi )\\\\r=(√(2463)√(\pi ))/(2\pi )\approx13.99997 \:cm`

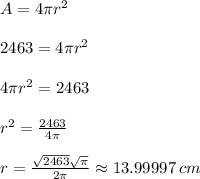
and the diameter is

`d=2\cdot (√(2463)√(\pi ))/(2\pi )=\sqrt{(2463)/(\pi )}\approx 27.9999 \:cm`