Question

According to the U.S. Bureau of the Census, the average age of brides marrying for the first time is 23.9 years with a population standard deviation of 4.2 years. A sociologist believes that young women are delaying marriage and marrying at a later age. The sociologist randomly samples 100 marriage records and determines the average age of the first time brides is 24.9 years. Is there sufficient evidence to support the sociologists claim at the level of significance of 1%

Answer 1

We conclude that young women are delaying marriage and marrying at a later age.

Explanation:

We are given that the average age of brides marrying for the first time is 23.9 years with a population standard deviation of 4.2 years.

The sociologist randomly samples 100 marriage records and determines the average age of the first time brides is 24.9 years.

Let
`\mu` = average age of brides marrying for the first time.

So, Null Hypothesis,
`H_0` :
`\mu` = 23.9 years {means that young women are not delaying marriage and marrying at a later age}

Alternate Hypothesis,
`H_A` :
`\mu` > 23.9 years {means that young women are delaying marriage and marrying at a later age}

The test statistics that would be used here One-sample z test statistics as we know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample average age of the first time brides = 24.9 years

`\sigma` = population standard deviation = 4.2 years

n = sample of marriage records = 100

So, the test statistics =
`(24.9-23.9)/((4.2)/(√(100) ) )`

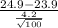
= 2.381

The value of z test statistics is 2.381.

Now, at 1% significance level the z table gives critical value of and 2.326 for right-tailed test.

Since our test statistic is more than the critical value of z as 2.381 > 2.326, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that young women are delaying marriage and marrying at a later age.