Answer:
The height is
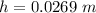
The kinetic energy during collision is not conserved
The Mechanical energy during the collision is not conserved
The mechanical energy after the collision is not conserved
Step-by-step explanation:
From the question we are told that
The mass of the block is
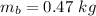
The mass of the wad of putty is
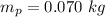
The speed o the wad of putty is
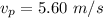
The law of momentum conservation can be mathematically represented as
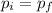
Where
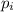 is the initial momentum which is mathematically represented as
is the initial momentum which is mathematically represented as
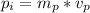
While
 is the initial momentum which is mathematically represented as
is the initial momentum which is mathematically represented as
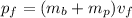
Where
 s the final velocity
s the final velocity
So
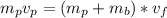
Making
 the subject
the subject
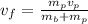
substituting values
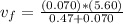

According to the law of energy conservation
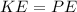
Where KE is the kinetic energy of the system which is mathematically represented as
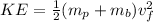
And PE is the potential energy of the system which is mathematically represented as
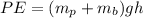
So
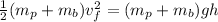
Making h the subject of the formula
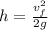
substituting values
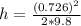
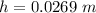
Now the kinetic energy is conserved during collision because the system change it height during which implies some of the kinetic energy was converted to potential energy during collision
The the mechanical energy of the system during the collision is conserved because this energy consists of the kinetic and the potential energy.
Now after the collision the mechanical energy is not conserved because the external force like air resistance has reduced the mechanical energy of that system