We have been given that part of the roof of a factory is devoted to mechanical support and part to green space. The area G that is designated as green space can be modeled by the polynomial
 and the area M that is devoted to mechanical support can be modeled by the polynomial
and the area M that is devoted to mechanical support can be modeled by the polynomial

We are asked to find the area of the green space, when area of roof (R) is 36 square yards.
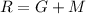

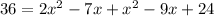
Let us solve for x.


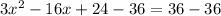
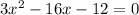
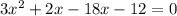
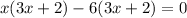
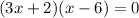
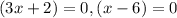
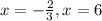
Since length cannot be negative, therefore, the value of x would be 6.
The area of green space would be:
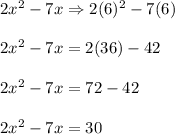
Therefore, the area of green space would be 30 square yards.