Question

In your own words, how do you create a residual plot that shows whether a linear model is an appropriate fit for the data?

Answer 1

For this case we assume that we have n pairs of observations
`(x_1 ,y_1) ,...,(x_n, y_n)`. Ad we have a model in order to estimate the real values
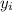`y_i` with a model. And the residuals are given by:

`e_i =y_i-\hat y_i`

Then we find the residuals for the n observations.

After that we can create a plot of
`(e_i , x_i) , i =1,2,...,n`.

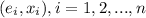Andd after create this graph if we see no pattern in the graph we can conclude that the linear pattern

Explanation:

For this case we assume that we have n pairs of observations
`(x_1 ,y_1) ,...,(x_n, y_n)`. Ad we have a model in order to estimate the real values
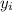`y_i` with a model. And the residuals are given by:

`e_i =y_i-\hat y_i`

Then we find the residuals for the n observations.

After that we can create a plot of
`(e_i , x_i) , i =1,2,...,n`.

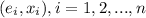Andd after create this graph if we see no pattern in the graph we can conclude that the linear pattern

Answer 2

Explanation:

We need to understand what residual plot is?

A residual plot is a graph that shows the residuals on the vertical axis and the independent variable on the horizontal axis.

Hence, there are 2 cases related to the relation between residual plot and a linear model:

1. If the points in a residual plot are randomly dispersed around the horizontal axis => the linear model is an appropriate fit for the data

2. If the points in a residual plot has a pattern => nonlinear model is more appropriate or the line have a bad fit with the set of the data.

Hope it will find you well.