Question

1. A company produces batteries. On average, 85% of all batteries produced are good. Each battery is tested before being dispatched, and the inspector correctly classifies the battery 90% of the time.

A. What percentage of the batteries will be “classified as good”?
B. What is the probability that a battery is defective given that it was classified as good?
(3+3=6 marks)

Answer 1

A. 78%

B. 1.92%

Explanation:

Given the information:

• 85% of all batteries produced are good
• The inspector correctly classifies the battery 90%

A. What percentage of the batteries will be “classified as good”?

The percentage of batteries are not good is:

100% - 85% = 15% and of those 100-90 = 10% will be classified as good. Hence, we have:

= 0.85*0.9 + 0.15*0.1 = 0.78

= 78%

So 78% of the batteries will be “classified as good”

B. What is the probability that a battery is defective given that it was classified as good?

We will use the conditional probability formula in this situation:

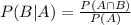`P(B|A) = (P(A \cap B))/(P(A))` where:

• P(A) is the probability of A happening. (A is classified as good) => P(A) = 78%

• P(B|A) is the probability of event B happening, given that A happened. (B classified as detective)

• 
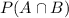  `P(A \cap B)` is the probability of both events happening =>
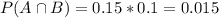  `P(A \cap B) = 0.15*0.1 = 0.015` (5% of the batteries are not good. Of those, 100-90 = 10% will be classified as good)

We have:

`P(B|A) = (P(A \cap B))/(P(A))` =
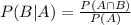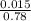`(0.015)/(0.78)` = 0.0192 = 1.92%

Hence, 1.92% probability that a battery is defective given that it was classified as good