Question

Develop 90 %, 95 %, and 99% confidence intervals for population mean (µ) when sample mean is 10 with the sample size of 100. Population standard deviation is known to be 5 1. Suppose that sample size changes to 144 and 225. Develop three confidence intervals again. What happens to the margin of error when sample size increases? 2. A simple random sample of 400 individuals provides 100 yes responses. Compute the 90%, 95%, and 99% confidence interval for population proportion (p). 3. With the same random sample as in 3, if the sample size increases to 1000, what happens to the three confidence intervals?

Answer 1

Explanation:

Hello!

Considering a certain population with normal distribution and the known population standard deviation σ= 51

From a random sample of n=100, the sample average resulted in X[bar]= 10.

The formula for the CI interval is:

[X[bar] ±
`Z_(1-\alpha /2)` *
`(Sigma)/(√(n) )`]

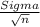90% CI

`Z_(1-\alpha /2)= Z_(0.95)= 1.64`

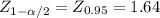
[10 ± 1.64 *
`(51)/(10)`]

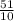[1.636; 18.364]

95% CI

`Z_(1-\alpha /2)= Z_(0.975)= 1.96`

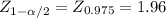
[10 ± 1.96 *
`(51)/(10)`]

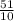[0.004; 19.996]

99% CI

`Z_(1-\alpha /2)= Z_(0.995)= 2.58`

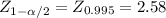
[10 ± 2.58 *
`(51)/(10)`]

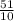[-3.158; 23.158]

1) The sample size has an indirect relationship with the amplitude of the interval, meaning that the bigger the sample size, the amplitude will decrease:

The population increases to n= 144

90% CI

`Z_(1-\alpha /2)= Z_(0.95)= 1.64`

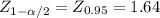
[10 ± 1.64 *
`(51)/(12)`]

[3.03; 16.97]

95% CI

`Z_(1-\alpha /2)= Z_(0.975)= 1.96`

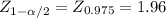
[10 ± 1.96 *
`(51)/(12)`]

[1.67; 18.33]

99% CI

`Z_(1-\alpha /2)= Z_(0.995)= 2.58`

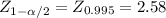
[10 ± 2.58 *
`(51)/(12)`]

[-0.965; 20.965]

The population increases to n= 225

90% CI

`Z_(1-\alpha /2)= Z_(0.95)= 1.64`

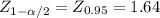
[10 ± 1.64 *
`(51)/(15)`]

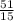[4.424; 15.576]

95% CI

`Z_(1-\alpha /2)= Z_(0.975)= 1.96`

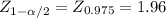
[10 ± 1.96 *
`(51)/(15)`]

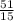[3.336; 16.664]

99% CI

`Z_(1-\alpha /2)= Z_(0.995)= 2.58`

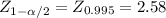
[10 ± 2.58 *
`(51)/(15)`]

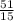[1.228; 18.772]

2) In this item the variable you have to estimate the population proportion of surveyed people that answered "yes"

[p' ±
`Z_(1-\alpha /2)` *
`\sqrt{(p'(1-p'))/(n) }`]

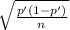Forr all intervals the sample proportion is p'= x/n= 100/400= 0.25

90% CI

`Z_(1-\alpha /2)= Z_(0.95)= 1.64`

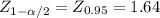
[0.25 ± 1.64 *
`\sqrt{(0.25*0.75)/(400) }`]

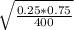[0.214; 0.286]

95% CI

`Z_(1-\alpha /2)= Z_(0.975)= 1.96`

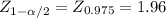
[0.25 ± 1.96 *
`\sqrt{(0.25*0.75)/(400) }`]

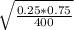[0.208; 0.292]

99% CI

`Z_(1-\alpha /2)= Z_(0.995)= 2.58`

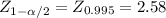
[0.255 ± 2.58 *
`\sqrt{(0.25*0.75)/(400) }`]

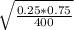[0.194; 0.306]

As you noticed in both CI, for the population mean and the population proportion, the confidence level has a direct relationship with the amplitude of the interval which means that the greater the confidence level of the interval, the wider its amplitude will be.

3) As mentioned before, the greater the sample size, the narrower the amplitude of the interval.

I hope it helps!