Question

A manufacturing company produces engines for light aircraft . The graph shows the number of engine produced each year since the company started operations. The data plot can be represented by the function . Base on the scatter plot , we can predict that in the ninth year , the company will produce Engines.

Answer 1

The data plot can be represented by the function .13 x + 32

Based on the scatter plot, we can predict that in the ninth year, the company will produce engines 149.

Explanation:

In the ninth year

13 (9) + 32

117 + 32 = 149

Answer 2

`y=13x+32`

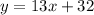
149 engines in 9th year

Explanation:

I think your question is missed of key information, allow me to add in and hope it will fit the original one.

Please have a look at the attached photo.

My answer:

From a look at the photo and the data plot can be represented by the function, so we can pick 2 points in our given graph

• (x1, y1) = (2,60)
• (x2, y2) = (5,99)

The standard form of a linear equation is:

y = mx + b where:

• m is the slope
• b is the y-intercept

We know the slope of the function can be found as following:

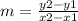`m = (y2 - y1)/(x2 - x1)` so in this situation we have:

<=>
`m=(99-60)/(5-2)=(39)/(3)=13`

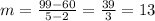
=> y = 13x + b (1)

Because the line goes through point (2,60) so we substitute it into (1):

60 = 13*2 + b

<=> b = 60 - 26 = 34

=> y = 13x + 34

Now we will substitute x=9 to find the engines produced by company in 9th year as:

`y=13(9)+32\\y=117+32=149`

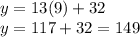
Hence, the company will produce 149 engines in 9th year