Question

Write a quadratic equation in standard form with x-intercepts (-3, 0) and (4, 0) that passes through (2, -20).

Answer 1

The equation in standard form is:
`y=2x^2-2x-24`

Explanation:

Since they give you the x-intercepts (the zeros of the quadratic expression) one knows that the binomials: (x-(-3)) and (x-4) must be factors of the quadratic expression.

We can therefore write the equation as:

`y=k\,(x+3)(x-4)`

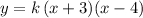
using the binomial factors given above, and a numerical factor "k" that we can determine by using the information that the graph passes through the point (2,-20):

`y=k\,(x+3)(x-4)\\-20=k\,(2+3)(2-4)\\-20=k\,(5)(-2)\\-20=k\,(-10)\\k=(-20)/(-10) \\k=2`

Then,the equation can be written as:

`y=2\,(x+3)(x-4)\\y=2(x^2-x-12)\\y=2x^2-2x-24`

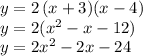
where we wrote the equation already in standard form