Question

A golfer hits a ball from a starting elevation of 5 feet with a velocity of 70 feet per second

down to a green with an elevation of -4 feet. The number of seconds t it takes the ball to
hit the green can be represented by the equation - 16t2 + 706 + 5 = -4. How long does it
take the ball to land on the green?
It takes the ball |
seconds to land on the green.

Answer 1

Time, t = 4.5 s

Explanation:

The number of seconds t it takes the ball to hit the green can be represented by the equation :

`-16t^2 + 70t + 5 = -4`

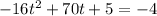
It means that the initial velocity is 70 ft/s. The above equation becomes:

`-16t^2 + 70t + 9=0`

It is required to find the time taken by the ball to land on the ground. It is a quadratic equation. The solution of quadratic equation is given by :

`t=(-b\pm √(b^2-4ac) )/(2a)\\\\t=(-b+ √(b^2-4ac) )/(2a),(-b- √(b^2-4ac) )/(2a)\\\\t=(-70+ √((70)^2-4* (-16)(9)) )/(2(-16)), \frac{-70-\sqrt{(70)^(2)-4*(-16)(9)}}{2(-16)}`

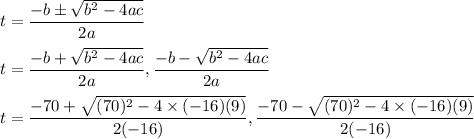
t = −0.125 and t = 4.5 s

Time cannot be negative. So, the time taken by the ball to land on the ground is 4.5 seconds.