Question

Find the confidence interval with a 90% level of confidence. In October 2010, Gallup Poll asked 510 randomly sampled adults the question, "Generally speaking, do you believe the death penalty is applied fairly or unfairly in this country today?" Of these, 58% answered "fairly", 36% said "unfairly" and 7% said they didn't know. (Percentages round up to 101% due to rounding) What percent of the population would consider the death penalty to be "fair"?

Answer 1

90% confidence interval for the percent of the population who consider the death penalty to be "fair" is [54.4% , 61.6%].

Explanation:

We are given that in October 2010, Gallup Poll asked 510 randomly sampled adults the question, "Generally speaking, do you believe the death penalty is applied fairly or unfairly in this country today?"

Of these, 58% answered "fairly", 36% said "unfairly" and 7% said they didn't know.

Firstly, the Pivotal quantity for 90% confidence interval for the population proportion is given by;

P.Q. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion who answered death penalty "fair" = 58%

n = sample of adults = 510

p = population percentage

Here for constructing 90% confidence interval we have used One-sample z test for proportions.

So, 90% confidence interval for the population percentage, p is ;

P(-1.645 < N(0,1) < 1.645) = 0.90 {As the critical value of z at 5% level

of significance are -1.645 & 1.645}

P(-1.645 <
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` < 1.645) = 0.90

P(
`-1.645 * {\sqrt{(\hat p(1-\hat p))/(n) } }` <
`\hat p-p` <
`1.645 * {\sqrt{(\hat p(1-\hat p))/(n) } }` ) = 0.90

P(
`\hat p-1.645 * {\sqrt{(\hat p(1-\hat p))/(n) } }` < p <
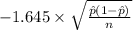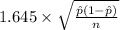`\hat p+1.645 * {\sqrt{(\hat p(1-\hat p))/(n) } }` ) = 0.90

90% confidence interval for p = [
`\hat p-1.645 * {\sqrt{(\hat p(1-\hat p))/(n) } }` ,
`\hat p+1.645 * {\sqrt{(\hat p(1-\hat p))/(n) } }`]

= [
`0.58-1.645 * {\sqrt{(0.58(1-0.58))/(510) } }` ,
`0.58+1.645 * {\sqrt{(0.58(1-0.58))/(510) } }` ]

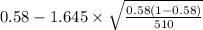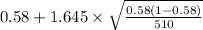= [0.544 , 0.616]

Therefore, 90% confidence interval for the percent of the population who consider the death penalty to be "fair" is [54.4% , 61.6%].