Question

In a game of luck, a turn consists of a player rolling 12 fair 6-sided dice. Let X = the number of dice that

land showing "l"in a turn.
Find the mean and standard deviation of X.
You may round your answers to the nearest tenth.

Answer 1

Answer: Mean: 2

Standard Deviation: 1.3

Explanation:

Answer 2

The mean of X, μₓ is 2

The standard deviation of X, σₓ is 1.3

Explanation:

Here we have the expected value given by the following relation

Expected value = P(x) × n

Where:

P(x) = Probability that the event occurs

n = Number of times the event occurs

The probability of the dice showing 1 = 1/6

The number dice rolled = 12

Therefore, out of 12, the expected number of dice that show 1 in a turn = 12×1/6 = 2

The proportion, p of dice that show 1 = 1/6, hence the mean, μx = np

Standard deviation of a proportion,
`\sigma _x =\sqrt{np{(1 - p)} }`

Where:

p = 1/6

n = 12

Hence;

μx = 12 × 1/6 = 2

`\sigma _x =\sqrt{np{(1 - p)} } = \sqrt{12 * (1)/(6) (1 - (1)/(6)) } = \sqrt{(5)/(3) } = 1.29099 \approx 1.3 \ to \ the \ nearest \ tenth`

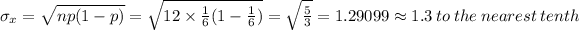
Hence the mean and standard deviation of X are presented as follows;

The mean of X, μₓ = 2

The standard deviation of X, σₓ = 1.3.