Answer:

Explanation:
To solve this, we need to use the discriminant.
Discriminant
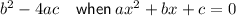

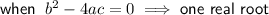
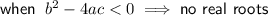
If the given equation has 2 real roots, then we need to use:
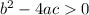
Given equation:

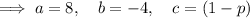
Substituting these values into
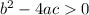 and solve for p:
and solve for p:
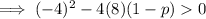
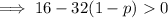
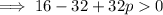
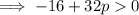
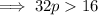

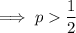
For the roots to be less than 1, first find the value of p when the root is 1.
If the root is 1, then
 will be a factor, so
will be a factor, so
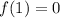
Substitute
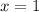 into the given equation and solve for p:
into the given equation and solve for p:
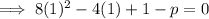
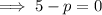
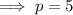
Therefore, the values of p for which the given equation has two different real roots less than 1 are:
