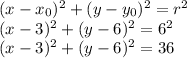Question

Find the equation of the circle that has a diameter with endpoints located at (-3,6) and (9,6)

Answer 1

The equation of the circle is:

`(x-3)^2+(y-6)^2=36`

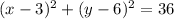
Explanation:

Notice that the points at the two extremes of the diameter they give you are both located along the line y=6, and are separated by each other the distance given by: 9-(-3) = 12. So the diameter of the circle is 12 units, and then its radius is half of that: 6 units. (r = 6).

Now the center of the circle must be located also on the line y=6, and its x position must be that of the equidistant point to the two extremes. that is: x center = 9-6 = 3

Then the center of the circle is at the point (3,6) in the plane.and its radius is r=6. With this info, we can use the standard equation for a circle of radius r and center
`(x_0,y_0)`:

`(x-x_0)^2+(y-y_0)^2=r^2\\(x-3)^2+(y-6)^2=6^2\\(x-3)^2+(y-6)^2=36`