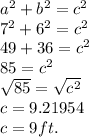Question

Can someone help me this will help me pass math :(? I need steps for both questions

Answer 1

A. You can not use the Pythagorean theorem because you would need the length of at least two sides but the triangle only provides the length of one.

B. x ≈ 7 ft. y ≈ 6 ft.

Explanation:

Sin(51) =
`(x)/(9)`

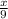
Sin(51)*9 = x

x = 6.99431

x ≈ 7 ft.

Now you can use the Pythagorean theorem.

`a^(2) +b^(2) =c^(2)`

`7^(2) +b^(2) =9^(2)`

`49+b^(2) =81`

`b^(2)` = 32

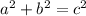
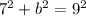
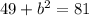
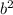`\sqrt{b^(2) } =√(32)`

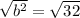
b = 5.65685

y ≈ 6 ft.

Or, continue to use the cosine.

Cos(51) =
`(y)/(9)`

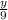
Cos(51)*9 = y

y = 5.66388

y ≈ 6 ft.

Answer Check

We know c = 9 ft.

`a^(2)+ b^(2)= c^(2) \\7^(2)+ 6^(2)= c^(2)\\49+36=c^(2)\\ 85 = c^(2) \\√(85) =\sqrt{c^(2) } \\c=9.21954\\c=9 ft.`