Question

A skateboarder starts at 33.7 m/s and comes to a stop in 9.62 s. How far does it
get?

Answer 1

324.194 m

Step-by-step explanation:

distance = speed × time

Answer 2

The skate boarder travels 162.2413 meters

Step-by-step explanation:

Notice that the skateboarder is traveling with with a stopping motion (negative acceleration since the velocity is reducing until it gets to zero - stopped final situation).

We can use the equation that relates velocity (v) with acceleration (
`a`), to find the value of such negative acceleration:

`change\,\,in\,\,velocity= a * t\\v_f-v_i=a* t`

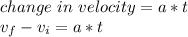
where the subindeces for the velocity (v) correspond to final and initial states.

In our case, the final velocity is zero (stopped), the initial velocity is 33.7 m/s, and the elapsed time is 9.62 seconds, therefore we can use this equation to find the acceleration "
`a`":

`v_f-v_i=a* t\\(0-33.7)\,(m)/(s) =a\,(9.62\,\,s)\\a=(-33.7)/(9.62) \,(m)/(s^2)\\a=-3.50\,\,(m)/(s^2)`

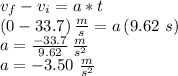
Now that we know the acceleration, we can estimate the distance covered in that time, using the position equation:

`Change\,\,in\,\,Position=v_i\,t+(1)/(2) a\,t^2\\Change\,\,in\,\,Position=33.7\,(9.62)\,+(1)/(2) (-3.50)\,9.62^2\\Change\,\,in\,\,Position=162.2413\,\,m`