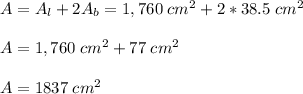Question

Ms. Calculation, the math teacher, has an 80 cm long rain stick that makes a sound like running water when she turns it upside down. When the students hear its sound, they know that it is a signal for them to be attentive listeners. Her rain stick is made of a big piece of bamboo for the long part of the cylinder and bamboo caps cover each end. It has a circumference of 22cm. What is the surface area of her bamboo rain stick?

Answer 1

The surface area of her bamboo rain stick is 1,837 cm^2

Explanation:

The bamboo rain stick can be modeled as a cylinder.

To calculate the surface of a cylinder, we add the lateral surface and 2 times the circular base.

`A=A_l+2A_b`

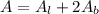
The lateral surface is equal to the length of the bamboo rain stick multiplied by the circunference of the base.

Then we have:

`A_l=l\cdot C=80\;cm\;\cdot 22\;cm=1,760\;cm^2`

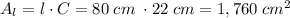
The base is calculated as π times the square of the radius. We don't know the radius, but we can calculate it from the circumference as:

`C=2\pi r=22\;cm\\\\r=(22\;cm)/(2\pi)\approx(22\;cm)/(6.28)=3.5\;cm`

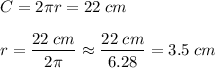
Then, we can calculate the base area as:

`A_b=\pi r^2\approx3.14(3.5\;cm)^2=3.14*12.27\;cm^2=38.5\;cm^2`

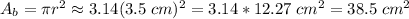
The surface area of the bamboo rain stick is:

`A=A_l+2A_b=1,760\;cm^2+2*38.5\;cm^2\\\\A=1,760\;cm^2+77\;cm^2\\\\A=1837\;cm^2`