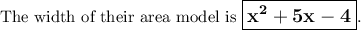Answer:
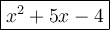
Explanation:
One way to make an area model for this question is:
- Divide a rectangle into three parts.
- Write the common factor on the left-hand side.
- Write one term of the polynomial in each box.
The area of each box is
A = lw. Then,
w = A/l
To get the width of each box, we divide its area by its length — the common factor, 4.
For the green box, w = 4x²/4 = x²
For the brown box, w = 20x/4 = 5x
For the yellow box, w = -16/4 = - 4
For the whole rectangle, w = x² + 5x - 4