Question

Consider the graph of the quadratic function y =

- 3x -
What are the roots of the function?
40.
-8 and 20
-40 and 8
–8 and 8
-40 and 20
| 4
12 16 20 24
Fhienet
Save and Exit​

Answer 1

A. -8 and 20

Explanation:

I think your question is missed of key information, allow me to add in and hope it will fit the original one.

Consider the graph of the quadratic function y =
`(1)/(4)`
`x^(2) - 3x - 40`

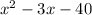
What are the roots of the function?

A. –8 and 20

B. –40 and –8

C. –8 and 8

D. –40 and 20

My answer:

Given the function:

y =
`(1)/(4)`
`x^(2) - 3x - 40`

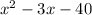
<=> y =
`x^(2) - 12x - 160`

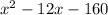
Let convert to the factors form, the roots of the function must meet the following requirements:

• The two number that has the sum of 12 = -b
• The two number that has the product of -40 = c

In 4 possible answer, only –8 and 20 is possible because:

-8 + 20 = 12 = -b

-8*20 = -160 = c

So the factored form of the function is:

y = (x + 8)(x-20)

Hope it will find you well.