Question

URGENT! Describe step by step how to find the following equations.

- Solve for x: cos x = sin x
- Solve for x: csc(x) + 3 = 1
- Solve for x: cot(3x) = -1
- Solve for x: 2sin²(x) + 3sin(x) = 2
- Solve for x: 4cos²(x) = 3
- Solve for x: 4sin³(x) + 1 = 2sin²(x) + 2sin(x)
(I know this is a little challenging, so whoever does it, you're the best!)

Answer 1

1. x = 45°

2. x = 330°

3. x = 105°

4. x = 30°

5. x = 60°

6. x = 30° or x = -45° (315°) or x = 45°

Explanation:

1. For

cos x = sin x

∴ sin x/(cos x) = 1 = tan x

Hence, x = tan⁻¹1 = 45°

2. For

csc(x) + 3 = 1

∴ csc(x) = 1 - 3 = -2

Which gives sin x = -1/2

∴ x = sin⁻¹(-1/2) = -30° = 360 +(-30) = 330 °

3. For

cot(3x) = -1

∵ cot(3x) = 1/(tan(3x))

Hence, 1/(tan(3x)) = -1

∴ tan(3x) = -1

3·x = tan⁻¹(-1) = -45° = 360 + (-45) = 315°

Which gives, x = -45/3 = -15° or x = 105°

4. For

2·sin²(x) + 3·sin(x) = 2

We put sin(x) = y to get

2·y² + 3·y = 2 or 2·y² + 3·y - 2 =0

Factorizing gives

(2·y -1)(y+2) =0

∴ y = 1/2 or y = -2

That is, sin(x) = 1/2 or sin(x) = -2

Hence, x = sin⁻¹(1/2) = 30° or x = sin⁻¹(-2) = (-π/2 + 1.3·i)

∴ x = 30°

5. For

4cos²(x) = 3 we have;

cos²(x) = 3/4

cos(x) = √(3/4) = (√3)/2

∴ x = cos⁻¹((√3)/2) = 60°

6. For

4·sin³(x) + 1 = 2·sin²(x) + 2·sin(x)

We put sin(x) = y to get;

4·y³ + 1 = 2·y² + 2·y which gives;

4·y³ + 1 - (2·y² + 2·y) = 0 or 4·y³ -2·y² - 2·y + 1 = 0

Factorizing gives;

`((2x-1)(2x+√(2)) )(2x-√(2)))/(2) =0`

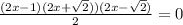
Therefore, x = 1/2 or x = -(√2)/2 or (√2)/2

Therefore, sin(x) = 1/2 or -(√2)/2 or (√2)/2

That is x = sin⁻¹(1/2) = 30 or sin⁻¹(-(√2)/2) = -45 or sin⁻¹((√2)/2) = 45.