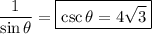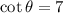Question

if cotθ= 7 and π < θ < 2π , sketch the angle θ and find the value of the other five trig functions

Answer 1

`\cot\theta=7`, so you immediately get

`\frac1{\cot\theta}=\boxed{\tan\theta=\frac17}`

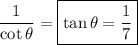
Recall the Pythagorean identity:

`\tan^2\theta+1=\sec^2\theta\implies\sec\theta=\pm√(1-\left(\frac17\right)^2)=\pm\frac{4\sqrt3}7`

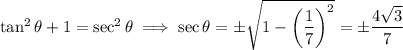
and from this we also get cosine for free, since

`\frac1{\sec\theta}=\cos\theta=\pm\frac7{4\sqrt3}`

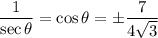
But only one of these can be correct. By definition of tangent,

`\tan\theta=(\sin\theta)/(\cos\theta)`

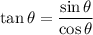
For
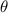`\theta` between π and 2π, we expect
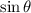`\sin\theta` to be negative. We konw
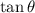`\tan\theta` is positive, which means
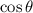`\cos\theta` must also be negative. So we have

`\boxed{\cos\theta=\frac7{4\sqrt3}}`

`\boxed{\sec\theta=\frac{4\sqrt3}7}`

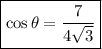
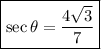
and we can find sine using the tangent:

`\tan\theta=(\sin\theta)/(\cos\theta)\implies\frac{\frac7{4\sqrt3}}7=\boxed{\sin\theta=\frac1{4\sqrt3}}`

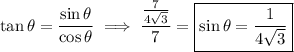
and for free we get

`\frac1{\sin\theta}=\boxed{\csc\theta=4\sqrt3}`