The correct answer is option a.)
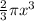 .
.
The formula for the volume
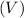 of a cone is given by
of a cone is given by
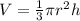 , where \(r\) is the radius of the base and
, where \(r\) is the radius of the base and
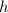 is the height. In this case, the height
is the height. In this case, the height
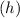 is twice the radius
is twice the radius
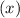 , so
, so
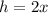 .
.
Substitute
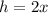 into the volume formula:
into the volume formula:
![\[V = (1)/(3) \pi r^2 (2x)\]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ctxkhtyxercwsux4n6qlswnzwqtqi937jn.png)
Simplify further:
![\[V = (2)/(3) \pi x^3\]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/z5opk7jyi6yk12o64prtu364na79ondelw.png)
Thus, the expression representing the volume of the cone is \(\frac{2}{3} \pi x^3\).
Therefore, the correct answer is:
a.
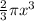
This expression accurately represents the volume of the cone in cubic units.