Question

Suppose in the triangle ABC below, AC is 5, and CD is 4. Find as many values as you can among the following:

Answer 1

`AD \approx 6.4\\BC= 4\\AB \approx 6.4\\\angle B = \angle D \approx 51.3\°`

Explanation:

The image attached shows the situation described in the problem.

Notice that we can use Pythagorean's Theorem to find AD, which is hypothenuse of the right triangle ACD

`AD^(2)=5^(2)+4^(2)\\ AD=√(25+16)\\AD= √(41)\approx 6.4`

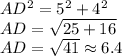
Additionally, triangle ABD is isosceles, its height is perpendicular bisector of side BD, that means BC = 4, and AB = 6.4.

Now, we can use trigonometric reasons to find angle D

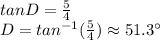
`tan D=(5)/(4)\\ D=tan^(-1)((5)/(4) ) \approx 51.3 \°`

And,
`B \approx 51.3 \°`, because it's an isosceles triangle.

Therefore, the values we found were

`AD \approx 6.4\\BC= 4\\AB \approx 6.4\\\angle B = \angle D \approx 51.3\°`