Question

Hello, I need help with a calculus FRQ. My teacher has given a hint that this last part has to do with the intermediate value theorem but I still am confused at where to start. Any help is appreciated. Thanks

Answer 1

Yes, at a time t such that (√2)/2 ≤ t ≤ 2.

Step-by-step explanation:

To answer the question

Therefore, where the domain of the function is the set of all real numbers x for which f(x) is a real number we have

For Chloe's velocity

`C(t) = t* e^(4-t^2) \ for \ 0\leq t\leq 2`

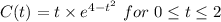
Finding the boundaries of the function gives;

`0* e^(4-0^2) = 0` and
`2* e^(4-2^2) = 2`

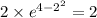
At t = 1, we have
`1* e^(4-1^2) = e^(3) = 20.086`

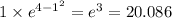
We find the maximum point as follows;

`\frac{\mathrm{d} \left (t* e^(4-t^2) \right )}{\mathrm{d} x}=0`

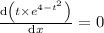
From which we have;

`\frac{\mathrm{} e^(4-t^2) - t* e^(4-t^2) *2* t }{(e^(4-t^2) )^2}=0`

`e^(4-t^2) - t* e^(4-t^2) *2* t }=0`

`e^(4-t^2)(1 - t*2* t })=0\\e^(4-t^2)(1 - 2* t^2 })=0\\`

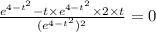
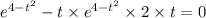
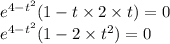
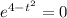`e^(4-t^2)=0` or
`(1 - 2* t^2 })=0`

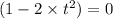
∴ 1 = 2·t² and from which t = (√2)/2

Hence the function C(x) is decreasing from t = (√2)/2 to t = 2

For Brandon

For 0 ≤ t ≤ 1, 1 ≤ B(t) ≤8 and for 1 < t ≤ 2, 8 < B(t) ≤ 1.5

1 ≤ f(x) ≤ 1.5

Given that the function B(t) is differentiable, therefore, continuous, there exists a point at which the function C(t) and B(t) intersects given that;

For 0 ≤ t ≤ (√2)/2, 0 ≤ C(t) ≤ 23.416 for (√2)/2 < t ≤ 2, 23.416 > C(t) ≥ 2

and for 0 ≤ t ≤ 0 1 ≤ B(t) ≤ 8 and for 1 < t ≤ 2, 8 > B(t) ≥ 1.5

Therefore, the curves intersect at in between (√2)/2 ≤ t ≤ 2.