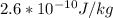Answer:
a) 0.0288 grams
b)
Step-by-step explanation:
Given that:
A typical human body contains about 3.0 grams of Potassium per kilogram of body mass
The abundance for the three isotopes are:
Potassium-39, Potassium-40, and Potassium-41 with abundances are 93.26%, 0.012% and 6.728% respectively.
a)
Thus; a person with a mass of 80 kg will posses = 80 × 3 = 240 grams of potassium.
However, the amount of potassium that is present in such person is :
0.012% × 240 grams
= 0.012/100 × 240 grams
= 0.0288 grams
b)
the effective dose (in Sieverts) per year due to Potassium-40 in an 80- kg body is calculate as follows:
First the Dose in (Gy) =
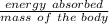
=
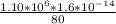
=
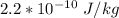
Effective dose (Sv) = RBE × Dose in Gy
Effective dose (Sv) =
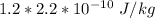
Effective dose (Sv) =