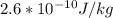Question

Potassium is a crucial element for the healthy operation of the human body. Potassium occurs naturally in our environment and thus our bodies) as three isotopes: Potassium-39, Potassium-40, and Potassium-41. Their current abundances are 93.26%, 0.012% and 6.728%. A typical human body contains about 3.0 grams of Potassium per kilogram of body mass. 1. How much Potassium-40 is present in a person with a mass of 80 kg? 2. If, on average, the decay of Potassium-40 results in 1.10 MeV of energy absorbed, determine the effective dose (in Sieverts) per year due to Potassium-40 in an 80- kg body. Assume an RBE of 1.2. The half-life of Potassium-40 is 1.28 x 10°years.

Answer 1

a) 0.0288 grams

b)
`2.6*10^(-10) J/kg`

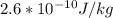
Step-by-step explanation:

Given that:

A typical human body contains about 3.0 grams of Potassium per kilogram of body mass

The abundance for the three isotopes are:

Potassium-39, Potassium-40, and Potassium-41 with abundances are 93.26%, 0.012% and 6.728% respectively.

a)

Thus; a person with a mass of 80 kg will posses = 80 × 3 = 240 grams of potassium.

However, the amount of potassium that is present in such person is :

0.012% × 240 grams

= 0.012/100 × 240 grams

= 0.0288 grams

b)

the effective dose (in Sieverts) per year due to Potassium-40 in an 80- kg body is calculate as follows:

First the Dose in (Gy) =
`(energy \ absorbed )/(mass \ of \ the \ body)`

=
`(1.10*10^6*1.6*10^(-14))/(80)`

=
`2.2*10^(-10) \ J/kg`

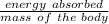
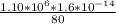
Effective dose (Sv) = RBE × Dose in Gy

Effective dose (Sv) =
`1.2 *2.2*10^(-10) \ J/kg`

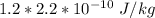
Effective dose (Sv) =
`2.6*10^(-10) J/kg`