Question

A cone-shape mountain of garden soil is dumped on a flat surface. If the diameter of the

mountain is 12 cm and its volume is 4800 cm cubed. how high is the mountain?

Answer 1

127.3 centimetres

Explanation:

The volume of a cone is denoted by:
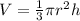`V=(1)/(3) \pi r^2h`, where r is the radius and h is the height.

Here, the diameter is 12, but remember that diameter is simply twice the radius. That means the radius is r = 12/2 = 6 cm.

We know the volume is V = 4800, so plug in these values to find h:

4800 = (1/3) * π * 6² * h

h ≈ 127.3 centimetres

Answer 2

127.4 cm

Explanation:

Diameter = 12 cm

Therefore, radius r = 12/2 = 6 cm

`V_(soil) = (1)/(3) \pi {r}^(2)h \\ 4800 = (1)/(3) * 3.14 * {6}^(2) * h \\ 4800 = (1)/(3) * 3.14 * 36 * h \\ 4800 = 3.14 * 12 * h \\ h = (4800)/(3.14 * 12) \\ h = (400)/(3.14) \\ h = 127.388535 \\ h = 127.4 \: cm \\`

Hence,height of mountain is 127.4 cm