Question

A credit card had an APR of 14.86% all of last year, and compounded interest

daily. What was the credit card's effective interest rate last year?

Answer 1

We have been given that a credit card had an APR of 14.86% all of last year, and compounded interest daily. We are asked to find the effective interest rate of the credit card.

We will use effective interest rate formula to solve our given problem.
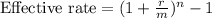`\text{Effective rate}=(1+(r)/(m))^n-1`, where

`r` = Annual interest rate in decimal form,

m = Number of times interest is compounded per year,

n = Number of compounding periods the rate is required for.

`14.86\%=(14.86)/(100)=0.1486`

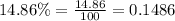
We need rate for 1 year, so n will be 365 times 1.

`\text{Effective rate}=(1+(0.1486)/(365))^(365\cdot 1)-1`

`\text{Effective rate}=(1+0.0004071232876712)^(365)-1`

`\text{Effective rate}=(1.0004071232876712)^(365)-1`

`\text{Effective rate}=(1.1601737274495528201)-1`

`\text{Effective rate}=0.1601737274495528201`

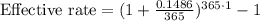
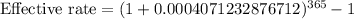
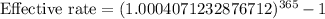
Let us convert effective rate in percent.

`0.1601737274495528201* 100\%=16.01737274495528201\%\approx 16.02\%`

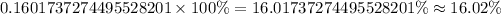
Therefore, the effective interest rate would be
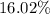`16.02\%`.