Find a formula for the function f(x) such that f'(x)=(cos(x))/(x)and f(1)=3.

Question

Find a formula for the function f(x) such that
`f'(x)=(cos(x))/(x)`and f(1)=3.

Answer 1

We want to find f(x) where f'(x) = cos(x)/x

Then we need to integrate f'(x) over x.

`f(x) = \int\limits {f'(x)} \, dx = \int\limits {(cos(x))/(x) } \, dx`

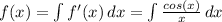
We must use a Taylor/McLauren polynomial to solve it.

Cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! .....

then the integral is:

`\int\limits {cos(x)/x \, dx = \int\limits {(1)/(x) - (x)/(2!) + (x^3)/(4!) .... \, dx`

`= lnIxI - (x^2)/(2*2!) + (x^4)/(4*4!) + .... (x^(2n) )/((2n)*(2n)!) + C`

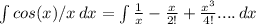
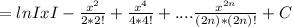
And we can write this as:

f(x) = lnIxI + ∑(-1)^n*(x^2n/(2n*(2n)!)) + C

fron n = 1 to n = ∞

and f(1) = 3.

ln(1) + ∑(-1)^n*(1/(2n*(2n)!)) + C = 3

∑(-1)^n*(1/(2n*(2n)!)) + C = 3

The sum, that is an alternating series and the terms are decreasing, so it converges, and the value can be obtained with a calculator, it is something around -0.24

-0.24 + C = 3

C = 3 - 0.24 = 2.76

f(x) = lnIxI + ∑(-1)^n*(x^2n/(2n*(2n)!)) + 2.76