Answer:
1
Explanation:
There are a couple of identities that come into play here:
a³ -b³ = (a -b)(a² +ab +b²)
(x^a)/(x^b) = x^(a-b)
(x^a)^b = x^(ab)
(x^a)(x^b) = x^(a+b)
_____
These mean we can simplify the expression as follows.
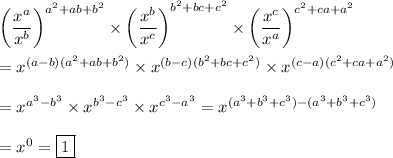
The expression has a value of 1.
__
Additional comment
For certain values of x and the exponents, the individual factors may exceed the ability of a calculator to express the value. That is, an attempt at numerical evaluation of this may produce a result different from 1. In any event, the expression is undefined for x=0.