Answer:
(5, 6)
Explanation:
First, get both equations into slope-intercept form so they are easier to graph:

The first equation is already in this form, so only do the second equation:
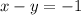
To do this, just solve for y and that should almost always get it in the correct form.
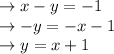
That equation is also now in slope-intercept form.
Now, using the slope and y-intercept in both equations, you can graph them. Using the graph, you can see the solution of this system of equations at (5, 6).