Question

Find the inequality represented by the graph.

Answer 1

`\displaystyle 4x + 3y < 15\:or\:y < -1(1)/(3)x + 5`

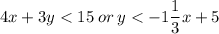
Explanation:

First, find the rate of change [slope]. From
`\displaystyle [3, 1],`travel three units west over four units north, where you will arrive at the y-intercept of
`\displaystyle [0, 5].`Doing this will lead you to knowing that the rate of change is
`\displaystyle -1(1)/(3).` Moreover, you could have also done this with the rate of change formula:

`\displaystyle (-y_1 + y_2)/(-x_1 + x_2) = m \\ \\ \\ (-1 + 5)/(-3 \pm 0) \hookrightarrow (4)/(-3) \\ \\ \boxed{-1(1)/(3) = m}`

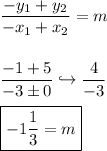
Here you are!

Now we insert this information into the Slope-Intercept formula, but BEFORE doing this, sinse we are dealing with the inequality version of the Slope-Intercept formula, we need to initiate the zero-interval test to determine the inequality symbol of the function. Here is how it is done:

`\displaystyle 0 < -1(1)/(3)[0] + 5; \boxed{0 < 5} \\ 0 > -1(1)/(3)[0] + 5; \boxed{0 \\gtr 5}`

Therefore, sinse this graph has a dashed line AND is shaded in the area that contains the origin, the less than symbol is suitable for this function, which means the slope-intercept inequality is
`\displaystyle y < -1(1)/(3)x + 5.`

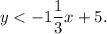
I am joyous to assist you at any time.