Question

Two small circles lie on the diameter of a larger circle as shown. If AB=24cm, what is the approximate area of the shaded region?

Answer 1

We have been given a diagram where two small circles lie on the diameter of a larger circle. The diameter of the large circle is 24 cm. We are asked to find the approximate area of the shaded region.

Since smaller circles are on diameter of larger circle, so the diameter of both smaller triangles will be half of 24 cm that is
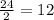`(24)/(2)=12` cm.

We know that radius is half the diameter, so radius of large circle will be 12 cm and radii of smaller triangles will be half of 12 that is
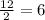`(12)/(2)=6` cm.

The area of shaded part will be area of larger circle minus sum of areas of smaller circles.

Area of circle formula:
`A=\pi r^2`

`\text{Shaded area}=\pi(12)^2-(\pi(6)^2+\pi(6)^2)`

`\text{Shaded area}=144\pi-(36\pi+36\pi)`

`\text{Shaded area}=144\pi-(72\pi)`

`\text{Shaded area}=72\pi`

`\text{Shaded area}=72(3.14)`

`\text{Shaded area}=226.08`

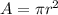
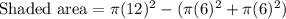
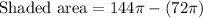
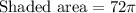
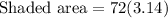
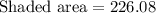
Therefore, the area of the shaded region is 226.08 square cm and option A is the correct choice.