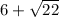Answer:
Explanation:
The quadratic formula is
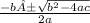
Ignore the weird A at the beginning, I don't know why it is there.
To get your equation into a quadratic equation, we have to move 12n to the other side, giving us
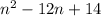
So in this case, our a=1, b=-12, and c=14. Remember
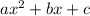
So we plug these values into our formula
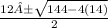 . Again, ignore the weird A.
. Again, ignore the weird A.
simplify and you will get
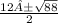
simplify the square root and you get

divide the
 and
and
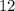 by the
by the
 on the bottom and you will get
on the bottom and you will get
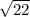 and
and
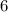
So your answers are
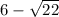 and
and