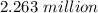Question

In an interest rate swap, a financial institution pays 10% per annum and receives three-month LIBOR in return on a notional principal of $100 million with payments being exchanged every three months. The swap has a remaining life of 14 months. The average of the bid and offer fixed rates currently being swapped for three-month LIBOR is 12% per annum for all maturities. The three-month LIBOR rate one month ago was 11.8% per annum. All rates are compounded quarterly. What is the value of the swap?

Answer 1

The correct answer to the following question will be "$2.263 million".

Step-by-step explanation:

In such a floating rate bond, the swap may be viewed as a long positioning paired with such a short squeeze in some kind of a fixed price bond. An appropriate discount rate through quarterly compound growth is 12 percent per annum or 11.8 percent annually with continuous compounding.

The floating rate loan would be worth $100 million right during the next deposit.

The next floating part would be:

⇒
`0.118* 100* 0.25`

⇒
`2.95`

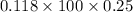
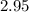
Therefore the floating rate value will be:

⇒
`2.5e^(-0.1182* 2/12) +2.5e^(-0.1182* 5/12)+2.5e^(-0.1182* 8/12)`

⇒
`2.5e^(-0.1182* 11/12)+102.5e^(-0.1182* 14/12)`

⇒
`98.678`

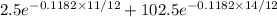
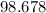
Now, Swap value:

⇒
`100.941-98.678`

⇒ $
`$2.263 \ million`

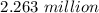
We should consider the swap as either a realistic approach to forward rate deals as just an alternative solution.

The estimated value is set to:

⇒
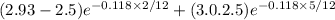
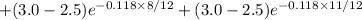
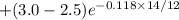
`(2.93-2.5)e^(-0.118* 2/12)+ (3.0.2.5)e^(-0.118* 5/12)`

⇒
`+(3.0-2.5)e^(-0.118* 8/12)+(3.0-2.5)e^(-0.118* 11/12)`

⇒
`+(3.0-2.5)e^(-0.118* 14/12)`

⇒ $
`2.263 \ million`