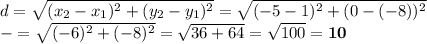Answer:
1. 3; 2. 12; 3. 5; 4. 13; 5. 10; 6. 10
Explanation:
We can use the distance formula to calculate the lengths of the line segments.
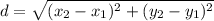
1. A (1,5), B (4,5) (red)
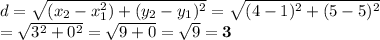
2. A (2,-5), B (2,7) (blue)
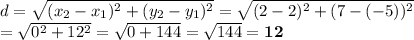
3. A (3,1), B (-1,4 ) (green)
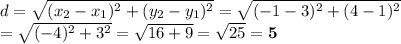
4. A (-2,-5), B (3,7) (orange)
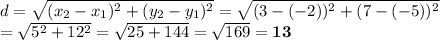
5. A (5,4), B (-3,-2) (purple)
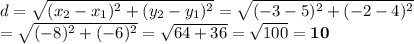
6. A (1,-8), B (-5,0) (black)